딥러닝을 공부하다 보면 기울기(Gradient) 라는 개념이 자주 등장합니다. 손실 함수가 최소가 되는 지점을 찾기 위해 경사 하강법(Gradient Descent) 을 사용한다고 하는데…
🤔 "근데 기울기가 왜 중요한 거야?"
🤔 "기울기 벡터가 방향을 가리킨다는데, 그 방향이 도대체 뭔데?"
오늘은 기울기 벡터가 어떤 의미를 가지는지, 그리고 이것이 어떻게 방향을 결정하는지 재밌게 알아보겠습니다! 🚀
📌 기울기 벡터란?
기울기 벡터(Gradient Vector)는 다변수 함수에서 각 변수에 대한 편미분 값을 모은 벡터입니다. 이 벡터는 함수를 가장 빠르게 증가시키는 방향을 가리킵니다.
예를 들어, 다음과 같은 함수가 있다고 해보죠.

이 함수는 **2차원 평면에서 볼록한 모양(볼록 함수, Convex Function)**을 띠고 있습니다. 즉, 가운데(0,0)에서 가장 낮고, 바깥쪽으로 갈수록 값이 증가합니다.
이제, 각 변수에 대해 편미분을 해보겠습니다.

이것을 벡터 형태로 정리하면?
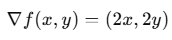
바로 이게 기울기 벡터입니다! 🎯
기울기 벡터는 항상 함수 값이 가장 빠르게 증가하는 방향을 가리킵니다!
🎢 기울기 벡터가 방향을 가리킨다고?
자, 기울기 벡터가 "함수가 가장 빠르게 증가하는 방향"을 가리킨다고 했습니다. 이게 무슨 의미일까요?
예를 들어, 점 (1, 2)에서의 기울기를 구해보면?

즉, (1, 2)에서는 (2, 4) 방향으로 이동하면 가장 빠르게 값이 증가한다는 뜻입니다! 🎯
반대로, 가장 빠르게 감소하는 방향은? 기울기의 반대 방향입니다! 즉, (-2,-4)
방향으로 이동하면 값이 감소하게 됩니다.
이 원리를 활용하면 경사 하강법(Gradient Descent)을 이해할 수 있습니다! 🚀
📉 경사 하강법: 기울기의 반대 방향으로 내려가기
딥러닝에서 우리는 손실 함수(Loss Function)의 값을 최소화하고 싶어 합니다. 즉, 기울기의 반대 방향으로 이동하면 최소값을 찾을 수 있습니다!
경사 하강법의 기본 수식은 다음과 같습니다.
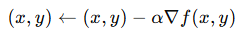

즉, 0.8, 1.6 방향으로 이동하면서 함수 값이 작아집니다!
반복해서 이 과정을 수행하면 결국 최솟값(0,0) 근처로 이동하게 됩니다. 🎯
🔥 결론: 기울기 벡터를 알면 방향을 알 수 있다!
✔ 기울기 벡터는 함수가 가장 빠르게 증가하는 방향을 가리킨다! ✔ 기울기의 반대 방향으로 이동하면 값이 감소한다! ✔ 경사 하강법(Gradient Descent)은 기울기의 반대 방향으로 이동하는 알고리즘이다!
🎯 즉, 딥러닝에서 최적의 가중치를 찾으려면, 기울기를 잘 활용해야 한다!
💡 이제 기울기가 왜 중요한지 감이 좀 오셨나요? 😆
딥러닝을 하면서 기울기를 보면 "아, 이게 어디로 이동해야 할지 가리키는 방향이구나!" 라고 생각하면 됩니다!
혹시 더 궁금한 점이 있다면 댓글로 남겨주세요! 🚀
'02. 딥러닝' 카테고리의 다른 글
| 00007. [AI 쉽게 이해하기 시리즈] RNN과 트랜스포머의 차이, 진짜 쉽게 설명해드립니다! (0) | 2025.04.03 |
|---|---|
| 00006. 🎢 딥러닝의 핵심: 경사 하강법과 역전파! (0) | 2025.03.19 |
| 00004. 최적화 알고리즘 비교: Momentum, AdaGrad, RMSprop, Adam (0) | 2025.03.11 |
| 00003. Learning Rate란? 머신러닝과 딥러닝에서의 역할 (0) | 2025.03.11 |
| 00002. 🚀 Sigmoid 함수를 쓰면 왜 기울기 소실(Gradient Vanishing)이 발생할까? (0) | 2025.03.10 |
