👋 안녕하세요! 오늘은 신경망에서 Sigmoid 함수를 사용할 때 기울기 소실(Gradient Vanishing) 문제가 왜 발생하는지에 대해 쉽고 재미있게 알아보겠습니다! 🧠✨
🎯 Sigmoid 함수, 너의 정체는?
Sigmoid 함수는 뉴런을 활성화(ON/OFF) 시키는 함수로, 아래와 같은 수식을 가지고 있습니다.

이 함수는 입력값 xx가 클수록 1에 가깝고, 작을수록 0에 가까워지는 특징을 가지고 있어요.
아래 그래프를 보면 더 이해하기 쉬워요! 👇
📈 Sigmoid 함수 그래프
- 가운데 부분에서는 부드럽게 변화하지만,
- 너무 큰 값이나 작은 값에서는 거의 변화가 없는 걸 볼 수 있어요!
⚠️ Sigmoid의 치명적인 문제: 기울기 소실(Gradient Vanishing)
🚧 1. Sigmoid의 미분값이 너무 작아져요!
신경망을 학습시키려면 **미분값(기울기, Gradient)**이 필요해요.
Sigmoid 함수를 미분하면 아래처럼 됩니다.
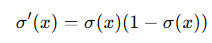
이 미분값을 살펴보면, 항상 0보다 크고 최대값이 0.25예요.
즉, 아무리 커도 0.25 이상 커질 수가 없어요! 😵
🔎 특히, xx가 너무 크거나 작으면?
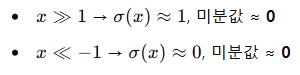
즉, 미분값이 거의 0에 가까워지는 문제가 발생해요.
🏗️ 2. 역전파에서 기울기가 점점 사라져요!
딥러닝에서는 역전파(Backpropagation)로 가중치를 업데이트하는데요,
여러 층을 거칠수록 미분값이 계속 곱해집니다.

Sigmoid를 쓰면 모든 층에서 최대 0.25가 곱해지니까,
층이 많아질수록 기울기가 거의 0에 수렴하는 문제가 발생해요! 😨
이걸 기울기 소실(Gradient Vanishing) 문제라고 해요! 🚨
❌ 기울기가 0에 가까워지면?
- 초기 층(입력층 쪽)은 학습이 거의 안 됨
- 가중치 업데이트가 느려지고, 모델이 제대로 학습되지 않음
💡 그럼 어떻게 해결할까요?
Sigmoid 함수의 단점을 극복하기 위해 여러 가지 대안이 등장했어요!
✅ ReLU (Rectified Linear Unit) 함수

- 음수는 0, 양수는 그대로 출력!
- 미분값이 0 또는 1이어서 기울기 소실 문제를 줄일 수 있음
✅ Leaky ReLU

- ReLU의 단점(음수에서 0이 되는 문제)을 해결한 버전
✅ Batch Normalization
- 입력값을 정규화해서 기울기 소실을 방지
🎯 정리!
❌ Sigmoid의 문제점
- 미분값이 최대 0.25로 작음
- 입력값이 너무 크거나 작으면 미분값이 거의 0
- 깊은 신경망에서는 기울기가 사라짐 → 학습이 제대로 안 됨
✅ 해결책
- ReLU, Leaky ReLU 같은 더 좋은 활성화 함수 사용
- Batch Normalization 적용
💡 앞으로 딥러닝을 구현할 때는 Sigmoid 대신 ReLU 같은 함수를 사용하는 게 더 좋겠죠? 😉
'02. 딥러닝' 카테고리의 다른 글
| 00006. 🎢 딥러닝의 핵심: 경사 하강법과 역전파! (0) | 2025.03.19 |
|---|---|
| 00005. 🎢 기울기 벡터는 어디로 가라고 하는 걸까? - 딥러닝의 비밀! (1) | 2025.03.19 |
| 00004. 최적화 알고리즘 비교: Momentum, AdaGrad, RMSprop, Adam (0) | 2025.03.11 |
| 00003. Learning Rate란? 머신러닝과 딥러닝에서의 역할 (0) | 2025.03.11 |
| 00001. Gradient Descent 완벽 정리: Batch GD, SGD, Mini-Batch 차이점 비교 (0) | 2025.03.06 |

